Welcome to my Blog
I am Francisco Ordòñez and I would like to introduce to you my blog. I am a student of Colegio Menor San Francisco De Quito, in Quito, Ecuador. My project here will be about linear and inverse variations. My role is to create a program that instructs children. Not just instruct in any way, it is in a way kids will like and enjoy,making them learn easier. I will use games and interesting questions of the topic.
The project will do many influence in kids. Normally kids do not like to learn to much, but with this game they will start learning and learning without anyone being at the back of them. This is mainly for kids and will teach them a lot, but also young adults can learn from it. Not just kids will be happy getting good grades, the parents will be happy too seeing how their sons and daughters enjoy doing math.
I created this blog to make more publicity and for more people to see this enjoying education. IN the blog there will be links to other programs. Like in excell you could enter into games and graph and even equations with processes . An other link will take you to see explications and processes to do find slopes, or the pater of the line. I hope you enjoy this blog.
Inverse Variations
Inverse variations are a type of variations that are not linear and never touch neither axis. They, in a graph show a line that is not linear and never touches zero because it involves division. The form of equation in the inverse variations is normally y=k/x, x=k/y and k=xy. This is the main information about inverse variations.
In the graph this variation never touches the line. It is because this variation involves division and multiplication of changing variables, so it will never touch the axes. The division is almost never negative because this variation most of the times is related to measures and measurements of figures. So, when you see a line in a graph that will never touch the axes it is probably an inverse variation.
The equations of inverse variations show very clearly that it is not linear. The equation of linear variations shows constant slopes and x and y intercepts. In the equations of inverse variation the equation is not with a constant slope, x intercept nor y intercept. As you can see linear and inverse equations are very different.
In the graph this variation never touches the line. It is because this variation involves division and multiplication of changing variables, so it will never touch the axes. The division is almost never negative because this variation most of the times is related to measures and measurements of figures. So, when you see a line in a graph that will never touch the axes it is probably an inverse variation.
The equations of inverse variations show very clearly that it is not linear. The equation of linear variations shows constant slopes and x and y intercepts. In the equations of inverse variation the equation is not with a constant slope, x intercept nor y intercept. As you can see linear and inverse equations are very different.
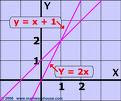
The Relationships between inverse and linear variations
Linear and inverse variations are very different, but they have some similarities. They are similar because they both have an equation that when put in a graph they form a line. This is the similarities but, the line of the inverse variations is completely different to the one of the linear variation. Also the equation is very different in both because they depend of different variables.
The lines of inverse and linear variations have nearly no similarity. The line of an inverse variation is a decreasing curve that will never cross any axes. In the other hand linear variations have a line that is straight, constant and that will always cross a least one axis. They both show completely different lines, one that's straight and one that's curvy, one that crosses the axis, one that will never cross the axis, etc.
The lines of inverse and linear variations have nearly no similarity. The line of an inverse variation is a decreasing curve that will never cross any axes. In the other hand linear variations have a line that is straight, constant and that will always cross a least one axis. They both show completely different lines, one that's straight and one that's curvy, one that crosses the axis, one that will never cross the axis, etc.
Linear and inverse variations have completely different equations. The equation of a linear variation has a constant slope, a changing independent variable, a independent variable and a starting point. In the equation of inverse variations there is a constant, a dependent variable and a independent variable. Both equations have a independent and a dependent variable but one has a slope, and one has no slope but it still forms a line so they are more different than alike.
Linear Variations
By graphing a linear variation a straight line shows up. It shows the special coordinates were it touches the axis and is never curving like in inverse variations. By looking at the line and having too exact points is necessary to find the equation. In the just typed paragraph it is obvious the difference to linear variations.
Linear variations have a equation that instantly you can graph. It has a slope that will go always constantly (m). It shows were the line starts, that is the b. And even you can find the constant and independent variable, that is the x. These are the main part of a linear equation.
Links and References
Information
In the following liks you will be able to learn more about linear and inverse variations.
This will talk about inverse variations: http://www.regentsprep.org/Regents/math/algtrig/ATE7/Inverse%20Variation.htm
The following link will be about linear variations:
http://en.wikipedia.org/wiki/Linear_equation
See also this link to learn:
http://www.sosmath.com/algebra/solve/solve0/solve0.html
Games
In the other hand, this are some games:
This game will involve solving equations.
http://www.mathplayground.com/wangdoodles.html
This game will involve graphing.
http://hotmath.com/games.html
This link will help you to get to the solutions of equations
http://www.math-play.com/Two-Step-Equations-Game.html
Bibliography:
Mainly my Math notebook.
Also some pages like:
Regents Prep Exam. Inverse Variation. Retrieved June 5, 2009 from: ........http://www.regentsprep.org/Regents/math/algtrig/ATE7/Inverse%20Variation.htm
Wikipedia. Linear Variation. Retrieved June 5, 2009 from: ..........http://en.wikipedia.org/wiki/Linear_equation
Link to so more information I did:
Suscribirse a:
Entradas (Atom)
